Découvrez Comment Retrouver Les Coordonnées Du Vecteur En Relation Avec La Base. Apprenez À Maîtriser Les Concepts Fondamentaux Pour Simplifier Vos Calculs Vectoriels.
**importance De La Base Pour Les Vecteurs**
- La Définition Fondamentale Des Vecteurs En Mathématiques
- L’importance De La Base Pour La Dimensionnalité
- Comment Choisir Une Base Pour Un Espace Vectoriel
- L’impact Des Bases Sur Les Transformations Linéaires
- Les Applications Pratiques Des Bases De Vecteurs
- Explorations Avancées : Bases Orthonormées Et Leur Utilité
La Définition Fondamentale Des Vecteurs En Mathématiques
Les vecteurs sont des éléments fondamentaux en mathématiques, souvent considérés comme des flèches ayant à la fois une direction et une magnitude. Quand vous pensez à un vecteur, imaginez une ligne qui s’étend dans un espace donné, reliant un point de départ à un point d’arrivée. Ils représentent des quantités physiques telles que la vitesse, la force ou le déplacement. Ainsi, chaque vecteur peut être représenté par des coordonnées dans un espace défini, ce qui facilite leur manipulation dans des équations et des applications.
La notion de base est cruciale pour les vecteurs, car elle offre un cadre permettant de décrire et de comprendre les relations entre eux. En choisissant une base appropriée pour un espace vectoriel, on est capable de décrire n’importe quel vecteur comme une combinaison linéaire de vecteurs de cette base. Cela revient à avoir une prescription claire, un script qui définit comment chaque vecteur peut être “composé” à partir des éléments constitutifs de base. Une compréhension approfondie de ce concept facilite également l’interprétation des transformations linéaires, qui sont essentielles dans de nombreux domaines des mathématiques et de la physique.
Il est fascinant de voir comment ces concepts mathématiques, bien que techniques, se retrouvent dans des situations courantes. Par exemple, dans le domaine médical, les vecteurs peuvent représenter la direction et l’intensité de certaines élixirs prescrits aux patients. En fait, l’analyse des médicaments, leurs interactions et leurs administrations impliquent souvent des vecteurs, de la même manière que la compréhension des forces en jeu dans divers systèmes. En somme, les vecteurs, par leur définition fondamentale, constituent des outils indispensables pour travailler dans divers domaines, tout en renforçant notre capacité à appréhender les dimensions complexes de notre environnement.
| Concept | Description |
|---|---|
| Vecteur | Quantité avec direction et magnitude |
| Base | Vecteurs de référence pour l’espace vectoriel |
| Transformation linéaire | Application qui modifie un vecteur tout en respectant la structure vectorielle |

L’importance De La Base Pour La Dimensionnalité
La base d’un espace vectoriel est cruciale pour saisir la dimensionnalité de celui-ci. Chaque vecteur peut être décrit par rapport à une base donnée, ce qui rend l’analyse mathématique non seulement plus simple, mais aussi plus puissante. Par exemple, pour les élèves découvrant le concept des transformations linéaires, comprendre comment un vecteur peut être exprimé en termes d’une base permet d’appréhender des notions plus complexes. En effet, deviner l’emplacement d’un vecteur dans un espace à plusieurs dimensions devient alors plus abordable, à condition de bien choisir ses fondations.
En plus de faciliter les calculs, une base adéquate aide à simplifier des opérations telles que l’addition et la multiplication scalaire. Pour illustrer cela, imaginons que nous souhaitons effectuer un changement de base, malgré la complexité apparente. Si on prend le temps de bien établir les relations entre les différentes bases, nous pouvons rapidement encontre as coordenadas do vetor em relação a base d’origine. Cela permet ainsi d’éviter une surcharge cognitive, ce qui est particulièrement utile pour les étudiants quand ils doivent naviguer entre différentes représentations.
Le choix d’une base est également déterminant dans la perception d’un espace vectoriel. Utiliser une base orthonormée, par exemple, offre des avantages indéniables en termes de simplicité de calcul et de compréhension visuelle. C’est dans cette sphère que la métaphore d’un “cocktail” délicatement mélangé prend tout son sens. Chaque élément doit être à sa place pour produire le résultat souhaité, tout comme les vecteurs dans leur espace. Sans une base adéquate, nous nous retrouvons face à une réalité mathématique qui semble chaotique et désordonnée.
Finalement, l’interaction entre les bases et la dimensionnalité nous montre que les mathématiques ne sont pas simplement une collection d’outils. Elles forment un langage complexe où chaque terme a un poids, une importance. Par la compréhension des bases et leur impact sur les vecteurs, nous développons une appréciation plus profonde de la structure mathématique. En effet, les bases ne font pas qu’exister dans des équations ; elles sont essentielles pour décrypter le monde des espaces vectoriels.
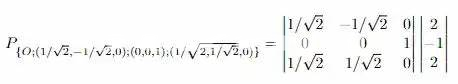
Comment Choisir Une Base Pour Un Espace Vectoriel
Choisir une base pour un espace vectoriel est un exercice qui combine à la fois rigueur mathématique et intuition. Pour commencer, il est essentiel de comprendre que la sélection d’une base influence comment on peut exprimer n’importe quel vecteur dans cet espace. En effet, chaque vecteur peut être écrit comme une combinaison linéaire des vecteurs de la base choisie. Cela signifie qu’il est crucial de s’assurer que les vecteurs de la base sont linéairement indépendants ; sinon, on risque de se retrouver avec des redondances qui compliquent inutilement la représentation des coordonnées.
Lorsqu’il s’agit de définir une base, il est fréquent d’opter pour des vecteurs qui s’adaptent bien aux dimensions de l’espace concerné. Par exemple, dans un espace à deux dimensions, deux vecteurs non colinéaires peuvent constituer une base efficace. Cela offre la possibilité de décrire toute position dans cet espace. En pratique, on peut utiliser des méthodes géométriques ou algébriques pour identifier les bonnes combinaisons de vecteurs qui serviront de base. En effet, si l’on cherche à encontre as coordenadas do vetor em relação a base, il est impératif de sélectionner des vecteurs qui s’alignent avec notre compréhension du phénomène étudié.
Un aspect intéressant à considérer est comment la base choisie peut affecter les calculs et les opérations effectuées sur les vecteurs. Certaines bases peuvent simplifier les calculs, tandis que d’autres peuvent les rendre plus complexes. Cela s’applique particulièrement aux transformations linéaires, où la représentation d’une transformation dans une base donnée peut révéler des caractéristiques essentielles de l’opération, mais aussi masquer certaines informations. Par conséquent, la sagesse populaire dans le monde mathématique stipule qu’il vaut mieux choisir une base qui rend les calculs aussi directs que possible.
Finalement, le choix d’une base se révèle également critique dans les applications pratiques. Que ce soit en physique pour modéliser des systèmes ou en informatique pour optimiser des algorithmes, la base utilisée peut influer significativement sur la performance globale. Ainsi, il n’est pas seulement question d’une simple formalité technique, mais d’une compétence essentielle dans le domaine mathématique. Les mathématiciens et ingénieurs doivent donc rester vigilants dans leur approche, s’assurant que chaque base qu’ils choisissent répond aux exigences de leurs projets tout en leur permettant d’explorer leur potentiel créatif.

L’impact Des Bases Sur Les Transformations Linéaires
Les transformations linéaires, essentielles en algèbre linéaire, sont influencées par le choix de la base d’un espace vectoriel. Lorsque vous voulez calculer une transformation, il est crucial de comprendre comment on encontre les coordonnées du vecteur en relation à la base choisie. Une bonne base permet non seulement de simplifier les calculs, mais aussi d’offrir une vision claire de la structure de l’espace. Par exemple, certaines bases facilitent la représentation graphique des vecteurs, rendant les transformations plus intuitives.
Lorsque l’on applique une transformation linéaire, les bases peuvent complètement changer le résultat. En manipulant les vecteurs selon une base spécifique, on peut révéler des propriétés cachées du système linéaire. Une transformation qui semble complexe peut être simplifiée considérablement si la bonne base est choisie, comparable à un medecin qui, en prescrivant un “elixir”, utilise le bon mélange de médicaments pour obtenir l’effet désiré. Chaque base offre sa propre perspective, influençant ainsi considérablement les résultats.
De plus, le choix de la base peut également affecter la manière dont nous comprenons des concepts avancés tels que la diagonalisation d’une matrice. La base appropriée permet de travailler avec des transformations plus simples, ce qui est particulièrement utile dans le cadre de l’optimisation et d’autres applications pratiques. Ainsi, comprendre l’impact des bases sur ces opérations est essentiel pour quiconque cherche à approfondir ses connaissances dans ce domaine.
Les Applications Pratiques Des Bases De Vecteurs
Dans le monde des mathématiques et de l’informatique, les bases des vecteurs jouent un rôle fondamental dans la résolution de problèmes complexes. Par exemple, lorsqu’on souhaite trouver des solutions à un système d’équations linéaires, la capacité à rencontre les coordonnées du vecteur en relation avec la base choisie est cruciale. Cela permet non seulement de simplifier les calculs, mais aussi d’optimiser les algorithmes utilisés dans diverses applications. Imaginez une firme qui doit gérer des milliers de prescriptions par jour : en utilisant des bases appropriées pour représenter les données, il devient possible de systématiquement identifier et traiter les prescriptions à l’aide d’un seul modèle théorique, réduisant ainsi le temps de “Count and Pour” et minimisant les erreurs.
Au-delà de l’informatique, les applications pratiques des bases de vecteurs se déploient dans divers domaines. Prenons l’exemple de la robotique : les bases de vecteurs sont essentielles pour définir les mouvements d’un robot dans un espace tridimensionnel. En choisissant des bases appropriées, un ingénieur peut facilement recalibrer le robot pour effectuer des tâches complexes avec une précision accrue. De plus, cet outil est indispensable en économie, où les bases aident à modéliser des systèmes économiques en transformant des vecteurs de données en informations exploitables. Dans ces contextes, le fait de travailler avec des bases correctement définies assure non seulement une plus grande efficacité, mais également une résolution rapide de problèmes, propulsant ainsi l’innovation à des niveaux sans précédent.
| Application | Domaine | Utilité |
|---|---|---|
| Gestion des prescriptions | Santé | Optimisation du traitement |
| Robotique | Ingénierie | Précision des mouvements |
| Modélisation économique | Économie | Analyse des données |
Explorations Avancées : Bases Orthonormées Et Leur Utilité
Les bases orthonormées sont essentielles dans le domaine des espaces vectoriels, car elles offrent une structure qui facilite de nombreuses opérations mathématiques. En effet, lorsqu’on travaille avec des bases orthonormées, chaque vecteur de l’espace peut être exprimé de manière unique en fonction des vecteurs de la base, ce qui simplifie les calculs. Cela se traduit non seulement par une meilleure clarté visuelle, mais aussi par une réduction des erreurs lors des opérations impliquant des transformations linéaires. En utilisant une base orthonormée, il est également possible de normaliser des vecteurs, un aspect qui est crucial dans des applications comme la représentation graphique ou la modélisation en trois dimensions où des calculs fréquents de distances et d’angles sont nécessaires.
Les applications pratiques des bases orthonormées s’étendent bien au-delà des théories mathématiques. Par exemple, dans le domaine de l’informatique, elles sont souvent employées pour le traitement d’images et d’audio, où elles permettent de coder efficacement des signaux. Par ailleurs, dans des secteurs tels que la physique et l’ingénierie, des représentations claires et précises des magnitudes et des directions aident à mieux gérer des systèmes complexes. Imaginez une clinque où le choix des vecteurs peut influer sur les résultats d’une substance, semblable à de la “Count and Pour”. En utilisant des bases appropriées, on maximise l’efficacité des résultats tout en minimisant les risques d’erreur, rendant ainsi ces systèmes plus robustes et fiables.